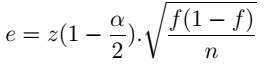Résumé d'échantillonnage et estimation
chapitre n°2 : Estimation
Bonjour, on continue notre résumé du cours échantillonnage et estimation avec le deuxième chapitre a savoir les estimations.
si vous avez des questions a propos de ce chapitre ou le chapitre precedent n’hésitez pas poser vos questions dans les commentaires ci-dessous.
bon courage.
1 Population
Sur une population on cherche a estimer sa moyenne m, sa variance (Écart type) 2 ( ); Ou sa proportion p.
comme exemple : estimer la taille moyenne des nouveaux nés au Maroc,estimer le poids moyen des filles ‡ une faculté, estimer le taux de chômage au Maroc ....
pour cette raison on a besoin d'un échantillon.
2 Échantillon
Comme tout le monde le sait, il n'est pas toujours possible d’étudier un caractère X sur toute la population, donc on va extraire juste un Échantillon et on cherche des informations sur lui.
3 Interprétation
[post_ad]
Sur une population on peut avoir sa moyenne m, sa variance (Écart-type) σ (σ"2 ); Ou sa proportion p:
De mémé pour l'échantillon il y a sa moyenne x̄ ; sa variance (Écart-type) s"2 (s); Ou sa fréquence f:
Exemple : On cherche a Étudier le poids chez des jeunes inscrits à la
Faculté A. Alors on a pris un Échantillon de taille 10 est on a obtenu ces résultats par Kg :
67.5 | 58.2 | 75.6 | 98.3 | 54.1 | 66.8 | 61.06 | 89.4 | 61 | 78.6 |
Alors la moyenne du poids de l’échantillon est
Et sa variance est
Donc on peut résumé les informations précédentes dans un tableau :
4 Estimation ponctuelle
Alors, comme on a vu, on cherche a faire une estimation d'une moyenne de population, variance , écart-type ou proportion, donc aussi on va le résumer dans un tableau.
5 Estimation par intervalle de confiance de la moyenne m
On commencera par Intervalle de confiance de la moyenne, mais avant cela nous allons voir trois exemples :
1. On cherche a estimer le poids moyen de sacs de farine sachant que le poids suit une loi normale avec un écart-type σ = 2g:
2. On cherche a estimer le poids moyen de sacs de farine sachant que le poids suit une loi normale N(m; σ ).
3. On cherche a estimer le poids moyen de sacs de farine.
Revenant a l'intervalle du confiance de la moyenne avec un risque :
x̄ est déjà calculé, mais e a 3 cas possible :
1. Si Loi connue et σ connue :
2. Si Loi connue et σ inconnue : on observe la taille n
donc 
3. Si Loi inconnue : on observe la taille n (Comme le 2Ème cas)
6 Estimation par intervalle de confiance de la proportion p
On commencera par deux exemple pour mieux connaitre la fréquence f :
1. On cherche a Étudier le taux de chômage au Maroc, donc on a pris un échantillon de taille 100 et on a trouvé parmi eux 32 chômeurs.
2. Pour savoir l'impact des affiches publicitaires d'une X société, sur un Échantillon de taille 275 personnes on a trouvé 21% qui s’intéresse ‡ ces affiches.
Dans le 1er cas on a
Dans le 2ème on a : n = 275 mais ici on a donné directement f = 0:21; car ce est sur l’échantillon.
Revenant a l'intervalle du confiance de la proportion avec un risque α :
avec
7 Taille de l’échantillon n : avec marge d'erreur e donnée.
On peut demander calculer la taille de l’échantillon dans deux cas :
1. dans le cas d'estimation de la moyenne m :
(a) Si est connue, alors
(b) Si est inconnue, alors
2. dans le cas d'estimation de la proportion p :
